The angular velocity formula describes how fast the object rotates or goes relative to another stage, i.e. how quickly the angular position or orientation of the object changes with time. Spin angular velocity describes how fast a rigid body rotates with respect to its center of rotation. Orbital angular velocity refers to how fast a point object revolves about a predetermined origin, i.e. the period rate of change of its angular position relative to the origin.
Generally, angular velocity is measured in angle per unit time, e.g. radians per minute. The SI unit of angular velocity is expressed as radians/sec together with the radian having a dimensionless value of unity, and hence the SI units of angular velocity are recorded as 1/sec.
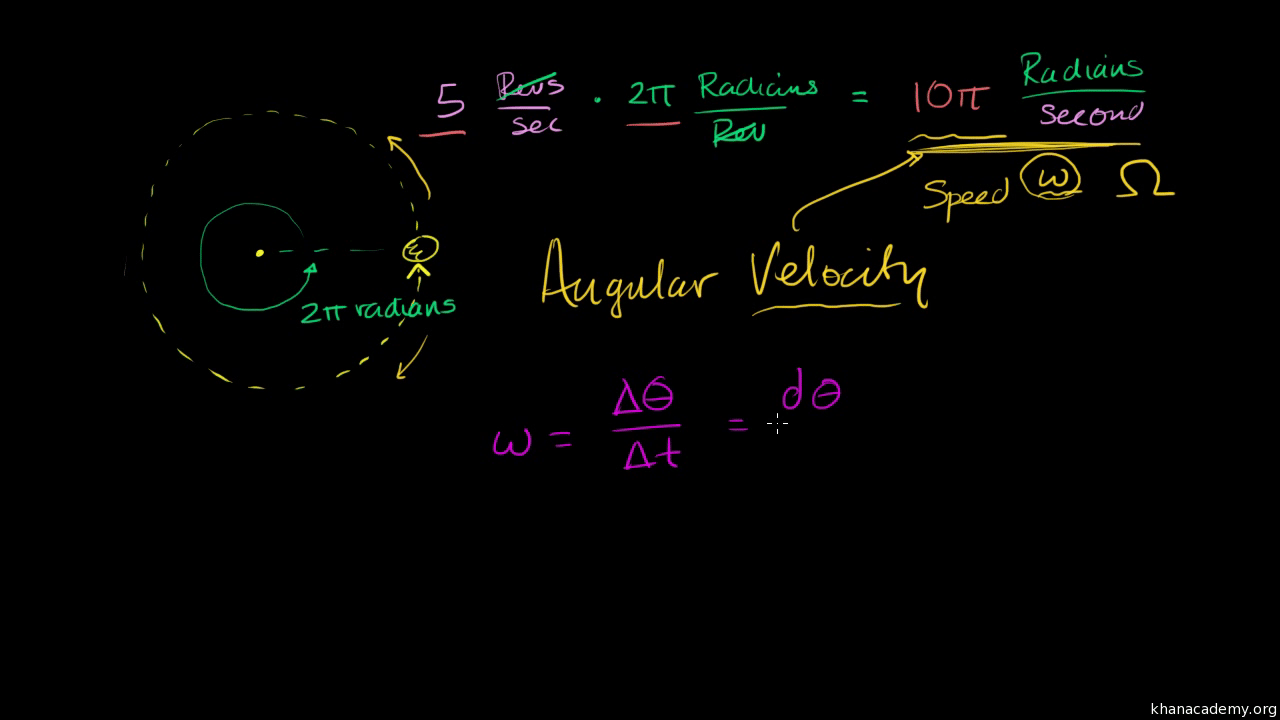
\Angular speed is usually represented by the symbol omega (ω, sometimes Ω). Angular speed is the speed of velocity at which an item or a particle is tilted around a center or a particular point in a given time period. It is also called rotational velocity. Angular velocity is measured in angle per unit time or radians per second (rad/s). Let us learn in more detail about the connection between angular velocity and linear velocity, angular displacement, and angular acceleration.
What’s Angular Velocity?
Angular velocity is a vector quantity and is called the rate of change of angular displacement which specifies the angular speed or rotational speed of an object and the axis where the object is rotating. The quantity of change of angular displacement of the particle at a given amount of time is known as angular velocity. The track of the angular velocity vector is perpendicular to the plane of rotation, in a direction that’s usually indicated by the numerical rule.
Angular Velocity Formula
To begin with, once you’re speaking about “angular” anything, be it speed or some other physical quantity, recognize that, because you’re dealing with angles, you are talking about traveling in circles or parts thereof. You may recall from geometry or trigonometry the circumference of a circle is its diameter instances the constant pi, or πd. (The value of pi is about 3.14159.) That is much more commonly expressed in relation to the circle’s radius r, which is half the diameter, which makes the circumference 2πr.
In addition, you’ve probably already heard somewhere along the way that a ring consists of 360 degrees (360°). If you move a distance S along a circle then the angular displacement θ is equivalent to S/r. One complete revolution, then, gives 2πr/r, which just leaves 2π. That means angles less than 360° can be expressed concerning pi, or in other words, as radians. Also Read – Horizontal Asymptote Rules and Definition
Taking All These pieces of data together, you are able to communicate angles, or portions of a circle, in units other than levels:
360° = (2π) radians.
1 radian = (360°/ / 2π) = 57.3°,
Whereas linear speed is expressed in length per unit time, angular speed is measured in radians per unit time, usually each minute.
Should you know that a particle is moving in a circular path with a speed v at a distance r in the middle of this circle, with the direction of v constantly being perpendicular to the radius of the circle, then the angular velocity may be written
Angular speed units are radians per minute; you might also treat this unit as “reciprocal moments,” since v/r yields m/s divided by m, or s-1, meaning that radians are technically a unitless quantity.
Angular velocity formulation in RPM
Revolutions Per Minute Programs
Revolutions per minute are also utilized to express how fast a circular thing such as a wheel spins. Since one revolution is equal to one complete rotation or spin about a center stage, a wheel that produces one complete rotation about its own center in a minute is said to rotate about its center at a rate of 1 revolution per second or one rpm. Because the next hand of a clock takes 1 minute to make one complete revolution about its center, it has a rotation speed of 1 revolution per second or one rpm. Suggestion – Alphanumeric Character | Definition & Characters